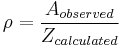Collision theory
Collision theory is a theory proposed by Max Trautz[1] and William Lewis in 1916 and 1918, that qualitatively explains how chemical reactions occur and why reaction rates differ for different reactions.[2] For a reaction to occur the reactant particles must collide. Only a certain fraction of the total collisions cause chemical change; these are called successful collisions. The successful collisions have sufficient energy (activation energy) at the moment of impact to break the existing bonds and form new bonds, resulting in the products of the reaction. Increasing the concentration of the reactants and raising the temperature brings about more collisions and therefore more successful collisions, increasing the rate of reaction.
When a catalyst is involved in the collision between the reactant molecules, less energy is required for the chemical change to take place, and hence more collisions have sufficient energy for reaction to occur. The reaction rate therefore increases.
Collision theory is closely related to chemical kinetics.
Contents |
Rate constant
The rate constant for a bimolecular gas phase reaction, as predicted by collision theory is:
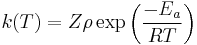 .
.
where:
- Z is the collision frequency.[3]
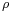 is the steric factor.[4]
is the steric factor.[4]- Ea is the activation energy of the reaction.
- T is the temperature.
- R is gas constant.
The collision frequency is:
where:
- NA is the Avogadro constant
- σAB is the reaction cross section
- kB is Boltzmann's constant
- μAB is the reduced mass of the reactants.
Quantitative insights
Derivation
Consider the reaction:
- A + B → C
In collision theory it is considered that two particles A and B will collide if their nuclei get closer than a certain distance. The area around a molecule A in which it can collide with an approaching B molecule is called the cross section (σAB) of the reaction and is, in principle, the area corresponding to a circle whose radius (rAB) is the sum of the radii of both reacting molecules, which are supposed to be spherical. A moving molecule will therefore sweep a volume 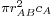 per second as it moves, where
per second as it moves, where 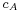 is the average velocity of the particle.
is the average velocity of the particle.
From kinetic theory it is known that a molecule of A has an average velocity (different from root mean square velocity) of 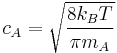 , where
, where 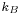 is Boltzmann constant and
is Boltzmann constant and 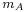 is the mass of the molecule.
is the mass of the molecule.
The solution of the two body problem states that two different moving bodies can be treated as one body which has the reduced mass of both and moves with the velocity of the center of mass, so, in this system 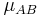 must be used instead of
must be used instead of 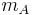 .
.
Therefore, the total collision frequency,[3] of all A molecules, with all B molecules, is:
From Maxwell Boltzmann distribution it can be deduced that the fraction of collisions with more energy than the activation energy is 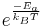 . Therefore the rate of a bimolecular reaction for ideal gases will be:
. Therefore the rate of a bimolecular reaction for ideal gases will be:
Where:
- Z is the collision frequency.
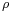 is the steric factor, which will be discussed in detail in the next section.
is the steric factor, which will be discussed in detail in the next section.- Ea is the activation energy of the reaction.
- T is the absolute temperature.
- R is gas constant.
The product Zρ is equivalent to the preexponential factor of the Arrhenius equation.
Validity of the theory and steric factor
Once a theory is formulated, its validity must be tested, that is, compare its predictions with the results of the experiments.
When the expression form of the rate constant is compared with the rate equation for an elementary bimolecular reaction, ![\scriptstyle r =k(T) [A][B]](/2012-wikipedia_en_all_nopic_01_2012/I/83d87be14e69236bd3c960b13efe888b.png) , it is noticed that
, it is noticed that 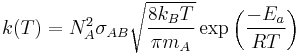 .
.
That expression is similar to the Arrhenius equation, and gives the first theoretical explanation for the Arrhenius equation on a molecular basis. The weak temperature dependence of the preexponential factor is so small compared to the exponential factor that it cannot be measured experimentally, that is, "it is not feasible to establish, on the basis of temperature studies of the rate constant, whether the predicted T½ dependence of the preexponential factor is observed experimentally"
Steric factor
If the values of the predicted rate constants are compared with the values of known rate constants it is noticed that collision theory fails to estimate the constants correctly and the more complex the molecules are, the more it fails. The reason for this is that particles have been supposed to be spherical and able to react in all directions; that is not true, as the orientation of the collisions is not always the right one. For example in the hydrogenation reaction of ethylene the H2 molecule must approach the bonding zone between the atoms, and only a few of all the possible collisions fulfill this requirement.
To alleviate this problem, a new concept must be introduced: the steric factor, ρ. It is defined as the ratio between the experimental value and the predicted one (or the ratio between the frequency factor and the collision frequency, and it is most often less than unity.[4]
Usually, the more complex the reactant molecules, the lower the steric factor. Nevertheless, some reactions exhibit steric factors greater than unity: the harpoon reactions, which involve atoms that exchange electrons, producing ions. The deviation from unity can have different causes: the molecules are not spherical, so different geometries are possible; not all the kinetic energy is delivered into the right spot; the presence of a solvent (when applied to solutions), etc.
| Experimental rate constants compared to the ones predicted by collision theory for gas phase reactions | |||
|---|---|---|---|
| Reaction | A (Azra frequency factor) | Z (collision frequency) | Steric factor |
| 2ClNO → 2Cl + 2NO | 9.4 109 | 5.9 1010 | 0.16 |
| 2ClO → Cl2 + O2 | 6.3 107 | 2.5 1010 | 2.3 10−3 |
| H2 + C2H4 → C2H6 | 1.24 106 | 7.3 1011 | 1.7 10−6 |
| Br2 + K → KBr + Br | 1012 | 2.1 1011 | 4.3 |
Collision theory can be applied to reactions in solution; in that case, the solvent cage has an effect on the reactant molecules and several collisions can take place in a single encounter, which leads to predicted preexponential factors being too large. ρ values greater than unity can be attributed to favorable entropic contributions.
| Experimental rate constants compared to the ones predicted by collision theory for reactions in solution[5] | ||||
|---|---|---|---|---|
| Reaction | Solvent | A 10−11 | Z 10−11 | Steric factor |
| C2H5Br + OH- | C2H5OH | 4.30 | 3.86 | 1.11 |
| C2H5O- + CH3I | C2H5OH | 2.42 | 1.93 | 1.25 |
| ClCH2CO2- + OH- | water | 4.55 | 2.86 | 1.59 |
| C3H6Br2 + I- | CH3OH | 1.07 | 1.39 | 0.77 |
| HOCH2CH2Cl + OH- | water | 25.5 | 2.78 | 9.17 |
| 4-CH3C6H4O- + CH3I | ethanol | 8.49 | 1.99 | 4.27 |
| CH3(CH2)2Cl + I- | (CH3)2CO | 0.085 | 1.57 | 0.054 |
| C5H5N + CH3I | C2H2Cl4 | - | - | 2.0 10−6 |
See also
References
- ^ Trautz, Max. Das Gesetz der Reaktionsgeschwindigkeit und der Gleichgewichte in Gasen. Bestätigung der Additivität von Cv-3/2R. Neue Bestimmung der Integrationskonstanten und der Moleküldurchmesser, Zeitschrift für anorganische und allgemeine Chemie, Volume 96, Issue 1, Pages 1 - 28, 1916, [1]
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "collision theory".
- ^ a b IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "collision frequency".
- ^ a b IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "steric factor".
- ^ Moelwyn-Hughes
External links
|
|||||||||||||||||
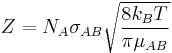
![N_A^{2} \sigma_{AB} \sqrt \frac{8 k_B T}{\pi \mu_{AB}}[A][B] =N_A^{2} r^{2}_{AB} \sqrt \frac{8 \pi k_B T}{ \mu_{AB}}[A][B] = Z [A][B]](/2012-wikipedia_en_all_nopic_01_2012/I/d57521a066ff17dcd36f6b20daca62ad.png)
![r = Z \rho [A][B] \exp \left( \frac{-E_{a}}{RT} \right)](/2012-wikipedia_en_all_nopic_01_2012/I/bb4fd45453eb7893a06f20e52fcf1e9e.png)